拓扑优化——水平集方法

发布时间：2024-06-24 15:22:52 丨 浏览次数：90

结构拓扑优化指：在同等工况下重新设计原有结构的分布，优化后的结构与原结构能够同时满足性能要求，强调的是"等价"。水平集方法是一种用于图像分割和轮廓提取的数学工具和计算方法。虽然它可能一开始看起来有点复杂，但实际上它是一个非常有用和强大的技术。

问题是什么：水平集方法主要用于解决图像分割问题。这意味着将图像中的不同对象或区域分开，通常通过找到它们的边界或轮廓。应用在拓扑优化里，就是不同材料的界面。

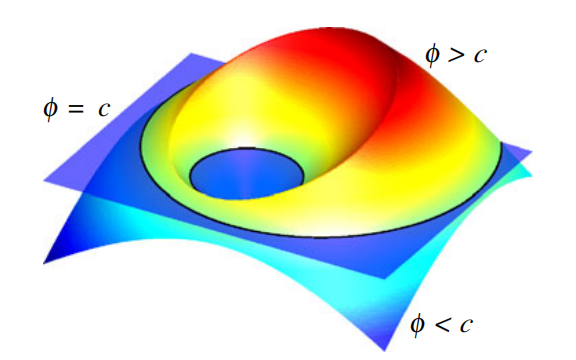
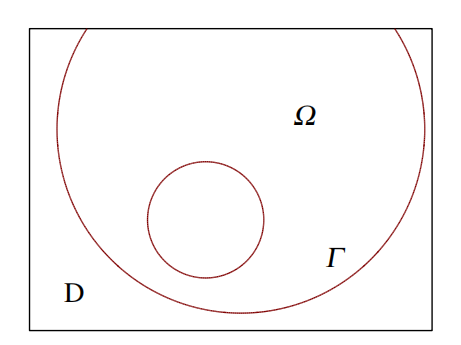
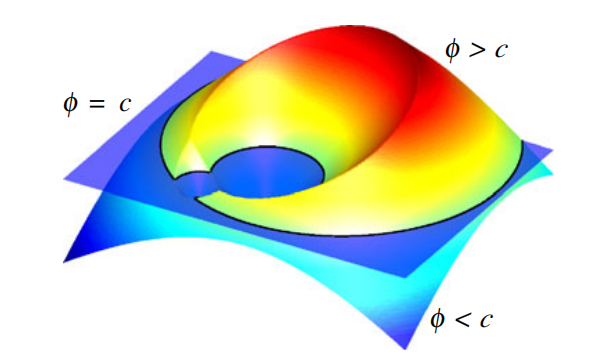
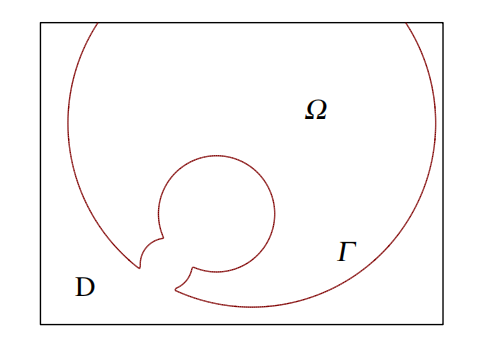
解决问题的方法：水平集方法使用数学上的水平集函数来表示图像中的对象边界。这个水平集函数是一个多维函数，其零水平集表示对象的边界。水平集方法很容易理解: 有一个弯曲的表面，它与一 个平面相交，给我们一个轮廓线，就是这样。通过演化方程，通常是古典的活动轮廓模型或者更现代的水平集方程，来移动水平集函数，使其逼近符合要求的理想轮廓。

哎呀，这里面居然涉及：传热方程(引入这个概念，作为势函数的演化方程，传热最终会达到平衡，演化也趋向最优解)，至于解这个传热方程，会用到了有限差分等方法，挺麻烦的，后续再写。