【路径规划】A*算法方法改进思路简析
A算法作为经典的传统路径规划算法,在计算全局最优路径有着较好的性能,在机器人导航等领域上起着关键作用,针对这点出发,将对A算法进行基本功能实现,以分析其优缺点,并在此基础上进行改进。改进的内容为,将针对特定地图的相关特点,设计合理的预估函数,设置了包含代价函数和启发函数的权重函数,其次,将传统的8方向搜索降为5个方向,舍弃无用的方向,然后在此基础上,对开放列表的数据结构进行堆优化,并且采用双向A算法进一步提高计算速度,并针对实际机器人运动过程中的路径不平滑问题采用贝塞尔曲线进行平滑化处理。经过仿真,改进后的算法在路径计算时间,路径平滑度都有改善,并进一步验证了A算法的可行性。这是我第一次尝试写文章,因此更像是一个笔记之类的东西,难免有错误与不妥之处,敬请指出与海涵。
A*算法作为Dijkstra算法和BFS的结合算法,其与这两种算法的区别就是采用了启发函数,这也是这个算法的核心。
启发函数的形式:
f
(
n
)
=
g
(
n
)
+
h
(
n
)
f(n)=g(n)+h(n)
f(n)=g(n)+h(n)
f
(
n
)
f(n)
f(n)表示结点的综合优先级,在选择结点时考虑该结点的综合优先级;
g
(
n
)
g(n)
g(n)表示起始点到当前结点的代价值;
h
(
n
)
h(n)
h(n)表示当前结点到目标点的代价估计值,也就是预估函数。
为了对这两个值进行相加,这两个值必须使用相同的衡量单位,以下的讨论也都是在此基础上进行的。
为了便于讨论与理解,下面的地图的形式都会已二维数组的形式表示。因此,为了简单预估当前节点到目标点的代价,采用较多的是欧几里得距离,即
d
i
s
=
(
x
1
?
x
2
)
2
+
(
y
1
?
y
2
)
2
dis = \sqrt{(x_1-x_2)^2+(y_1-y_2)^2}
dis=(x1??x2?)2+(y1??y2?)2?
A*算法通过设置两个列表openlist和closelist来对地图中的点进行控制。算法伪代码如下:
在A*算法的总体流程中提到,A*算法的核心就是启发函数,根据式(1),其中的 g ( n ) g(n) g(n)作为起始点到当前点的代价,其值一般是固定的,所以围绕启发函数的优化一般都是围绕 h ( n ) h(n) h(n)即预估函数展开的。
前面提到,对于二维网格地图,一种常用的预估函数就是应用欧几里得距离。但是,需要注意的是,如果机器人的运动并不是无限制的,或者说是不允许无角度限制的进行运动,例如:当机器人被设定为只允许沿八方向运动时,此时欧氏距离并不能准确描述当前点到终点的运动代价,因为机器人不允许按这种方式直接抵达,而此时采用切比雪夫距离则可以更准确的描述运动代价。
切比雪夫距离公式:
d
i
s
=
m
a
x
(
∣
x
1
?
x
2
∣
,
∣
y
1
?
y
2
∣
)
dis = max(|x_1-x_2|,|y_1-y_2|)
dis=max(∣x1??x2?∣,∣y1??y2?∣)
同样的,如果当机器人只允许沿四个方向运动,那么曼哈顿距离更能准确描述运动代价。
曼哈顿距离公式:
d
i
s
=
∣
x
1
?
x
2
∣
+
∣
y
1
?
y
2
∣
dis=|x_1-x_2|+|y_1-y_2|
dis=∣x1??x2?∣+∣y1??y2?∣
如果h(n)能够更为准确的描述当前点到终点的代价,那么就可以使在依赖启发函数f(n)进行选点时更加准确。
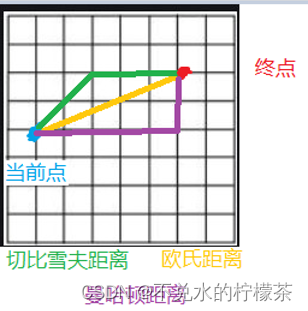
所以,针对实际的工作需求,确定合适的
h
(
n
)
h(n)
h(n)是十分重要的,预估函数越贴近实际的路径代价,其选点准确度越高,但也需要注意h函数的复杂程度,过于复杂的预估函数会极大的提高计算量,造成运算速度减慢。
关于预估函数另一个方面的优化是改进启发函数的权重系数,对于A*算法的基本原理,不难将其理解为Dijkstra算法和BFS的综合应用, 其中Dijkstra算法的主要思想是通过实际代价找到当前的最优路径或是其大致方向,而BFS的主要思想是考虑实际代价以快速扩展当前点的周围节点,最后通过预估函数和实际代价的和确定一个搜索方向。
再回到我们对启发函数的定义,不难发现启发函数就是代价函数与估计函数1:1的和,但是,如果我们更改实际代价与预估代价的权重,就可控制A*算法更偏向于实际代价或是预估代价,例如将代价权重改为2:1,即
f
(
n
)
=
2
?
g
(
n
)
+
h
(
n
)
f(n)=2*g(n)+h(n)
f(n)=2?g(n)+h(n),此时,f(n)会更偏向描述实际代价,也就是会更优先考虑当前路径已造成的代价,所以f会更贴近于Dijkstra算法,当我们推广这个结论,当g(n)>> h(n)时,就相当于f(n)只考虑实际代价而完全不考虑预估代价,即退化为Dijkstra算法。反之,若g(n)的权重系数小于h(n)的权重系数,则会优先考虑预估代价,做同样的推广,当h(n)>> g(n)时,A*算法此时不依靠实际代价控制搜索方向,因此所得结果可能不是最短路径。
因此,调整实际代价与预估代价的权重,可以有效地减少搜索点,提高搜索速度。
为了便于考虑,我们可以将启发函数改为如下形式,即在预估函数前增加一个系数w,从而改变启发函数的权重
f
(
n
)
=
g
(
n
)
+
w
?
h
(
n
)
f(n)=g(n)+w*h(n)
f(n)=g(n)+w?h(n)
进一步的,我们不可能只考虑搜索速度而不考虑规划的路径,此时就考虑使用动态加权的方式,以原本的启发函数h(n)为判断依据,我们把它声明为d,当高于某个值时,将w增大,此时算法搜索速度更快;当d小于某个值时,将权值降低,也就是接近终点的时候,优先考虑最优路径。这个阈值的考量因素包括CPU的速度、用于路径搜索的时间片数、地图上物体的数量、物体的重要性、难度或者其他任何因素来进行动态的选择。w的值也要根据自己设定地图的大小、复杂程度进行多次调节,也可以按实际情况设置多段加权。
最后,利用这个阈值使算法在准确性和快速性之间的抉择是一般局部的,全局范围只采用一个权重效果一般不如局部的好。
另一个导致低性能的原因来自于启发函数的结点处理,当某些路径具有相同的f(n)值的时候,它们都会被搜索,尽管只需要搜索其中的一条,所以我们希望能从这样启发函数值相同的节点中做出取舍。
而取舍的方式就是为预估函数增加一个微小的偏移量p,这个偏移量p能起作用的原因是:当某两个节点的启发函数值相同时,我们希望优先判断那个距离终点更近的节点,而距离终点近也就意味着其预估函数值更小,所以,如果我们为预估函数增加一个小偏移量p(p甚至可取0.1%左右),就会使得距终点近的的节点的启发函数值更小,就会被优先选择。因此,我们可以将启发函数进一步优化为如下形式
f
(
n
)
=
g
(
n
)
+
h
(
n
)
?
(
w
+
p
)
f(n)=g(n)+h(n)*(w+p)
f(n)=g(n)+h(n)?(w+p)
此处邻域的优化是以八方向的运动机器人为基础进行改进的,其他运动形式的机器人在改进思路上是类似的,都是尽可能的减少搜索方向,或者增大每次比较中的选择范围,来降低计算量。
对于八方向的运动机器人,其父子节点的位置关系只能如图2所示
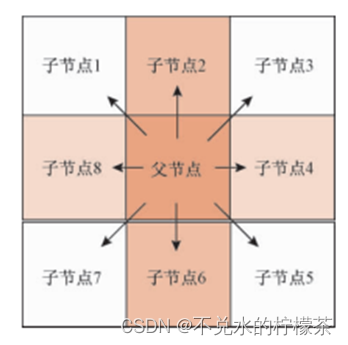
所以对于某些地图来说,我们很容易发现某些方向是不可能成为最优路径的一部分,如图3,所以对这个图来说,子节点1、7、8都不需要被搜索,因此在遍历时这三个方向可以直接被舍弃掉。
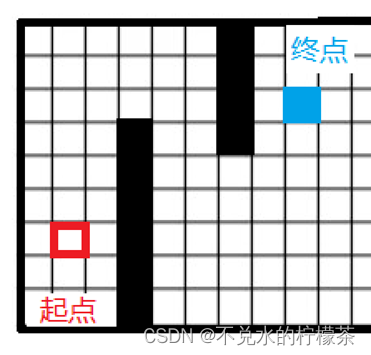
对上面的情况进行推广,不难发现,我们选择舍弃哪三个方向,只取决于起点和终点的位置,用一种参数化的方法进行描述就是根据目标点与当前点的夹角对搜索方向进行分类,分类的结果如表2。
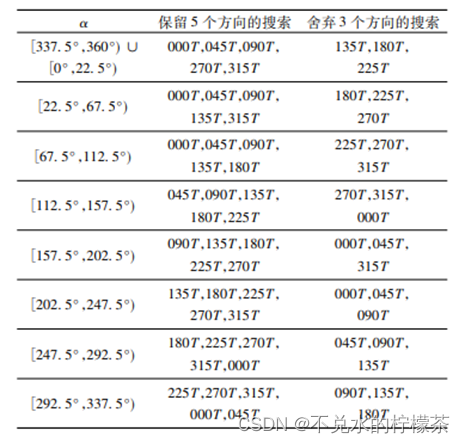
表中参数α表示的是起点与终点方向的连线与正北方向的夹角。
对这种方法的总结性的描述,这种方法会舍弃八个方向中的三个方向,因为这三个方向的选点一定会使路径代价升高,所以可以不考虑从而降低计算量,但是这种方法受地图本身类型的影响比较大,某些构造的地图采用这种方法性能提升并不明显,甚至可能出现卡死错误,因此可将其作为某些局部的优化方法,或者对邻域舍弃规则根据具体需要做进一步改进。
扩展邻域法的思想是通过提高单次邻域的搜索范围,从而减少整个过程中的搜索次数,从而降低计算量。图4所示的方法就是把8搜索邻域扩展为32邻域,其他扩展方法包括扩展为16邻域、24邻域、48邻域等。
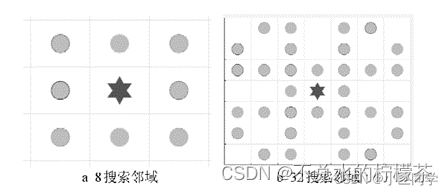
但是,这种方法同样对于地图有限制要求,如果障碍物范围过小,扩展邻域法可能会出现轨迹穿墙问题,因为此时的轨迹不再是一格一格计算出来的,而是一次计算好几个格的前进距离。
双向搜索的简要过程:
使用两个A*搜索,称为Astar1和Astar2
(1)Astar1从起点出发,Astar2从终点出发
(2)Astar1以Astar2的open表中的F值最小的栅格为终点进行扩展;
(3)Astar2以Astar1的open表中的F值最小的栅格为终点进行扩展;
(4)若Astar1或Astar2的open表为空,表示找不到,退出;
(5)重复(2)(3)(4) ,直到两个A搜索都到达终点,此时两者相遇,表示成功找到路径,退出;
值得注意的是,双向A算法的计算方法并不是计算当前点到终点的路径,而应该规划的是从当前点到另一侧的openlist表中的最小值点的路径,这样才能保证正反两个方向的路径最终一定会相交。
此外,双向A*不需要保证正反“同步”,完全可以一个方向快一个方向慢,至于具体那边快和慢,就应该具体问题具体分析。
一种思路是,两侧的openlist每次只优先处理openlist中节点数少的那个,这样可以保证最终的所搜索到的总结点数会降低。
Openlist列表是A*算法中需要频繁进行插入、比较的容器,在openlist上我们主要有三种操作:主循环重复选择最好的结点并删除它;访问邻居结点时需要检查它是否在集合里面;访问邻居结点时需要插入新结点。因此,我们可以尝试通过优化openlist的数据结构,加快新元素插入或是比较过程的速度从而达到优化的效果。
作为很简单的两种数据结构,数组删除一个元素或者查找最值都需要花费O(n),插入一个新节点只需要O(1);而链表删除一个元素或插入新元素只需要花费O(1),而链表查找一个极值节点需要花费O(n)。
由2.4.1可知,未排序数组查找一个最值的特定节点花费的代价是比较大的,因此,我们可以选择将数组进行排序操作,这样在查找时,就可以使用二分查找,使查询过程的时间复杂度降低为O(logn)。但是,如果要维护数组的有序性,那么插入新元素的代价也会上升,其时间复杂度为O(n)。
在排序数组中,插入操作是很慢的,所以可以通过链表结构来加快插入的速度。但是同样的,使用链表结构会导致集合关系检查的代价上升,因为不能使用二分查找了,只能遍历整个链表,使得花费上升为O(n)。
总的来说,排序链表查找并删除最值元素只需要O(1),但对于新元素的插入操作仍然需要O(n)的代价。
2.4.3中提到,有序链表由于不能使用二分查找,只能进行逐个遍历从而找到新元素的位置,因此,为了解决普通链表进行集合关系查找效率低下的问题,可以采用跳表来代替链表。
跳表的一个结构简图如图5
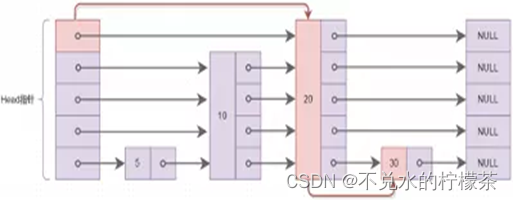
以图5为例,跳表在进行集合关系检查时,是不需要遍历每个元素的,例如我们需要查找30,我们可以从头节点直接跳跃到元素20,再查找30,而这个过程中,元素5和10是没有被遍历的。这种查找方式类似于二分法,因此,普通链表的查询时间复杂度为O(n),而跳表的时间复杂度O(logn)。
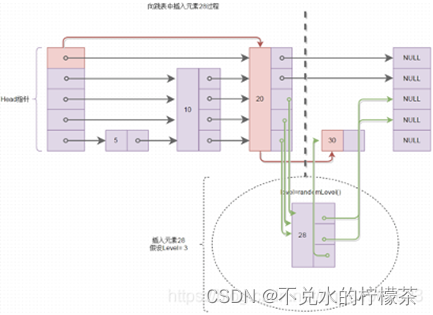
而向跳表中插入元素,由于元素所在层级的随机性,平均起来也是O(logn),也就是查找元素应该插入在什么位置,然后就是普通的移动指针问题。图6所示是往跳表中插入元素28的过程,图中红色线表示查找插入位置的过程,绿色线表示进行指针的移动,将该元素插入。
哈希表使用一个哈希函数将地图上的每一个节点映射到一个哈希码上,并使哈希表的大小等于结点数的2倍,以降低哈希冲突的可能性。假设哈希函数时间复杂度为O(1),那么集体关系检查的时间复杂度、插入操作、删除的时间复杂度都是O(1)。但是这种方法是以时间换空间,对于特别大的地图就会浪费特别大的空间以创建哈希表。
二叉堆是一种保存在数组中的树状结构,与普通的二叉树不同,二叉堆是可以通过索引查找节点的。
我们使用二叉堆的原因是,前面大部分数据结构都采用了有序性这一特点,这是为了能更在O(1)时间内找到其中的最大值或最小值,而实际上,集合内部元素是否有序对我们算法来说是没有影响的,我们关注的只有最值,所以采用二叉堆就是一个很好的选择。以大根堆为例,当我们需要删除最大的元素时,直接移除堆顶元素即可。
总的来看,二叉堆的插入和删除操作花费都为O(logn),维护相对有序性的花费也是O(logn).
因此,使用二叉堆对降低A*算法的时间复杂度有很大的帮助。
关于数据结构的优化,关注整体算法的时间复杂度是十分必要的,但是,我们也需要关注小常数下算法的行为,不同的数据结构在不同的数据量下表现出的速度性能也未必与渐进行为下的速度的比较结果保持一致,某些更复杂的数据结构或许在数据量极大的情况下能表现出很好的性能,但是在小规模数据下却不一定比简单的数据结构的运行速度更快,因此,对于数据结构的选择是需要根据实际问题的规模进行权衡和进一步分析的,没有哪一种数据结构能够一劳永逸的解决所有问题。
对于网格地图来说,直接应用A*算法得到的最终路径存在着折线线段多,折线角度大等问题,考虑到移动机器人实际工作环境及相关运动参数后,这些问题也将很大的影响机器人的工作效率,因此,我们需要对A*算法得到的路径进行平滑化处理,从而达到消除折线段和减小折线角度的问题。
因此,可以采用贝塞尔曲线法或B样条曲线法来达到这一目的。下面将以贝塞尔曲线法为例,对路径进行平滑化处理。
贝塞尔曲线是应用于二维图形应用程序的数学曲线。以二阶贝塞尔曲线为例,其取点的方法是:在两条线段上找两个能等比例平分两条线段的点,并在其连线上找到能等比例平分这条连线的点,该点即为贝塞尔曲线上的一点,改变比例,就能得到贝塞尔曲线上的其他点,这些点组成的曲线即为贝塞尔曲线。
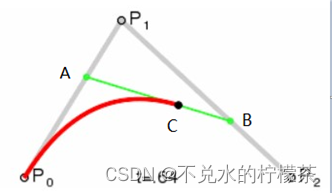
以图7为例,有
二阶贝塞尔曲线公式:
![B=〖(1-t)〗^2 P_0+2t(1-t) P_1+t^2 P_2,t∈[0,1]](https://img-blog.csdnimg.cn/fd6c0d7608e842f8accbf53d0ef04788.png)
高阶贝塞尔曲线公式:
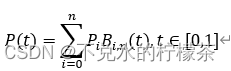
利用贝塞尔曲线公式可以对二段及多段折线进行平滑化处理,所以,我们可以利用高阶贝塞尔公式对路径中所有的折线进行平滑化处理,从而使最后的路径平滑连续。
将贝塞尔曲线应用在A*算法上,其关键在于修改贝塞尔曲线的控制点,我们将A星算法最终运行得到的节点两个列表中的值作为控制点,得到折角处的贝塞尔曲线。
测试地图为7070的网格地图,初始点为(-6,-6),终点(50,50),机器人半径为1,地图构建如图8
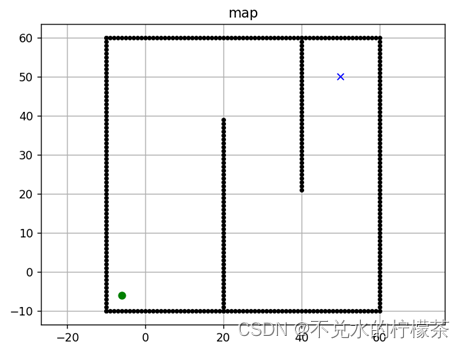
机器人移动规则:允许沿8个方向进行移动,其中上下左右四个方向的代价都为1,斜向运动代价都为√2。
图例:以黑色圆点表示障碍物;青色叉表示已经被纳入过openlist的点,最终路径以红色线进行表示。
首先是对A算法的源程序进行测试,测试结果如图9
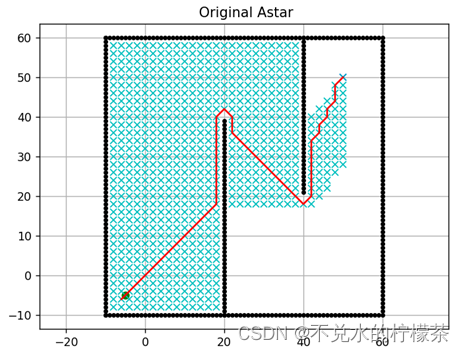
用时:3677ms
注意到,本例中机器人虽然是允许八方向移动,但是水平垂直移动和斜向移动代价并不相同,因此预估函数并不适合使用切比雪夫距离,而是继续采用欧氏距离。
权重系数与偏移量;
为预估函数增加一个简单的2段动态加权,当h(n)>18 时,权重系数w=3,当h(n)≤18时,权重系数w=0.8 。偏移量p始终取0.1%。结果如图10。
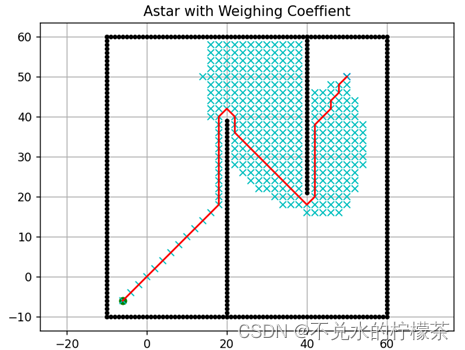
用时:1354ms
可以看到,权重系数的加入,使得算法在距离终点很远时可以不必一直追求最优路径,而是优先选择快速使预估代价降低,从而避免了遍历大量的不必要节点,极大的提高了算法的运行速度。
由地图我们很容易得到,图二中子节点1、7、8都不需要被搜索,因此在遍历时这三个方向可以直接被舍弃掉,从而降低计算量。
不采用权重系数和采用权重系数的结果图分别如图11、图12
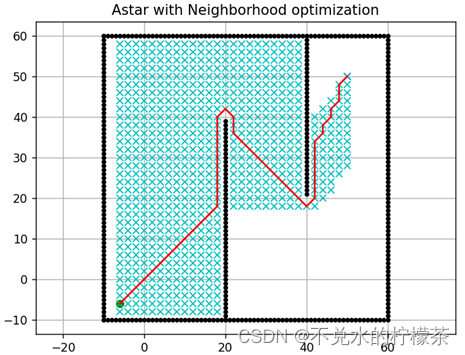
用时:3583ms

用时:1302ms
由上述结果可知,删减邻域法可以将某些绝对不可靠的路径点加以剔除,但是对本例来说,性能提升有限,因为起本例点的位置导致了处理的点不可能向左侧大范围扩展。因此可以得出结论,删减邻域法可以提升算法性能,但受地图本身性质影响较大,实际操作时可能不会将其作为必要的改进手段进行考虑。
依照上述改进手段将原本的八邻域扩展为32邻域进行测试,测试结果如图13所示。
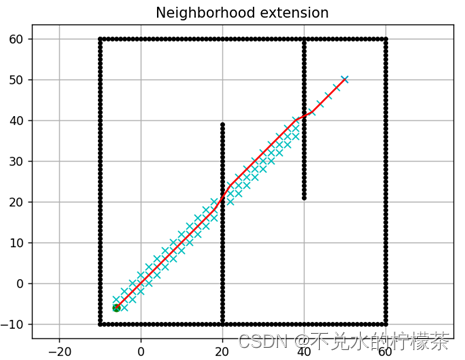
可以发现,邻域扩展法在面对体积较小的障碍物时会发生穿墙的现象,也就是导致程序忽略较小的障碍物。即便我们在增大墙的宽度之后,程序就可以同图14运作,但在经过墙角时还是会发生穿越障碍物的现象。
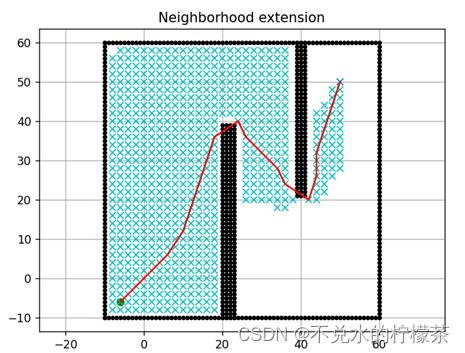
用时:3391ms
因此可以得出,对邻域的优化都是在对地图有一定已知信息时才能发挥较好的优化效果。
此处采用贝塞尔曲线法对最终路径做平滑处理,红色线为原路径,蓝色线为贝塞尔曲线法优化后的路径,结果如图15
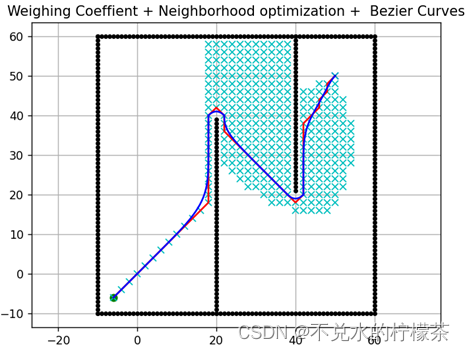
可以看出,贝塞尔曲线法在对折线的平滑化方面有着很好的效果。此外,B样条曲线法、微分平坦等方法在对折线平滑化方面都有着很好的效果。
依照2.3步骤将单侧A算法改写为双向A,未应用权重系数和应用权重系数的双向A*算法计算结果分别如图16、17。
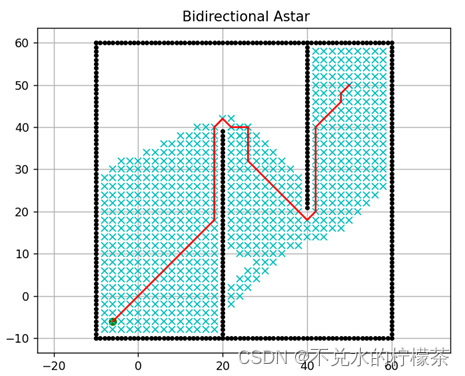
用时:1792ms

用时:2738ms
由上图不难得出,双向A*算法对算法整体性能的提升也很有帮助,但是经过图16和17的比较,发现在双向A*中采用权重系数后,速度却不如只采用双向A*。
我猜测原因可能是,当两个方向的操作点相互靠近时,两点间的预估代价小于动态加权所规定的阈值,导致算法的速度开始下降,但是距离实际两点之间的正确路径还有较大距离(例如两个操作点在墙的两侧),导致运行时间变长。
因此,将3.2中动态加权的阈值由18改为10,这样可以使得两点开始精确计算时,两点的距离降低,结果如图18
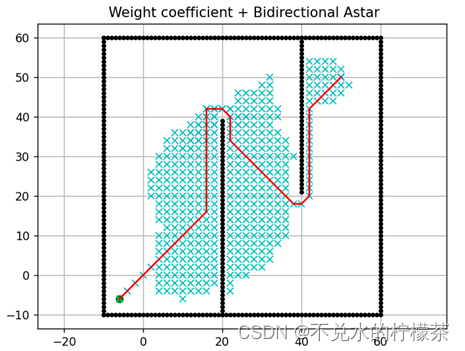
用时:996ms
由上可得,双向A*算法在降低算法运算时间方面有着很好的效果,而在和权重系数同时作用时可进一步降低计算量。但是需要注意的是,动态加权的参数必须根据实际地图的特点或是实际问题具体设置,没有一个参数可以一劳永逸的解决所有问题,必要时,应该设置针对实际情况的连续的动态权重系数,而不能简单的进行多端加权。
通过以上改进手段,我们不难得到一个简单的优化该算法的方法,即利用改进启发函数、搜索邻域、曲线平滑化和采用双向A算法进行综合改进,之所以此处不使用堆优化方法对数据结构进行改进的原因是本例中地图尺寸不是很大,对数据结构的优化效果并没有很明显,而对于数据量极大的地图来说,采用堆优化方法或者是更复杂的数据结构就显得很有必要了。本例最终改进结果如图19。

用时:1037ms
可以发现,改进后的A算法在计算速度上相比于原来的3677ms得到了极大的提升。同时,最终路径也更加平滑,这将更有利于实际机器人的运动流畅性。
A算法作为传统路径规划算法中比较常用的一种,其在静态地图下有着很好的性能,优化的思路主要是围绕着A算法的核心——启发函数进行的。此外,从算法过程中,储存容器的数据结构也是很重要的一环,另外,通过从单向BFS到双向BFS进行的优化,从中可以推广到双向A*算法,这对原本算法的性能也是极大的提高。最后,在得到结果路径后,选择合适的方法使结果路径更加平滑,这将更有利于机器人的实际工作。
代码
https://github.com/myveibae/Astar-and-Bidirectional-Astar
[1]吴飞龙,郭世永. 融合改进 A* 和动态窗口法的 AGV 动态路径规划[J]. 科学技术与工程,2020,20( 30) : 12452-12459
[2]魏博闻, 严华. 一种面向非结构化环境的改进跳点搜索路径规划算法[J]. 2021.
[3]秦锋,吴健,张学锋,赵晶丽.基于A*的双向预处理改进搜索算法.计算机系统应用,2019,28(5):95-101
[4]金世俊, 柴引引. 一种基于改进A*算法和贝塞尔曲线的全局路径规划方法:, CN112683278A[P]. 2021.
[5]王淼弛. 基于A*算法的移动机器人路径规划[D]. 沈阳工业大学.
[6] 唐平,杨宜民.动态二叉树表示环境的A*算法及其在足球机器人路径规划中的实现[J].中国工程科学,2002,4(9):50-53.
网站
https://www.bilibili.com/video/BV1FL4y1M7PM?spm_id_from=333.999.0.0&vd_source=a4cdb4f1cff245b6b6fc13bbb2a96641
扫一扫关注微信公众帐号
